Is the Transition from Univariate to Multivariate Gaussian Distribution Linear?

Background

In the previous Chapter 0 and Chapter 1 of this column, we explored foundational concepts like the covariance matrix and the correlation matrix, which are key building blocks in understanding relationships between multiple variables. Building on that, this chapter introduces the multivariate Gaussian distribution, a central concept that plays a pivotal role in many areas of statistical modeling and machine learning. While this distribution has broad applications, from image processing to finance, it is particularly important in the context of Gaussian processes, which we will explore further in upcoming chapters.

The multivariate Gaussian distribution is a natural extension of the univariate normal distribution to higher dimensions, providing a simple yet powerful way to model the relationships between multiple variables. In the context of Gaussian processes, it is used to model the underlying distributions of functions, helping us make predictions about unknown values based on observed data.

The Multivariate Gaussian Distribution

Univariate Gaussian Distribution: Revisiting the Basics

To set the stage, let’s recall the form of the one-dimensional Gaussian distribution. The probability density function (PDF) for a random variable \(x\) that follows a normal distribution with mean \(\mu\) and variance \(\sigma^2\) is given by:

At its core, this function describes the probability that a random variable \(x\) will take a particular value, given that it is normally distributed around a mean \(\mu\) with variance \(\sigma^2\). The bell-shaped curve of the Gaussian distribution is symmetric around \(\mu\), with the spread determined by \(\sigma\). The exponential term \(\exp \left( -\frac{(x - \mu)^2}{2 \sigma^2} \right)\) captures how the probability decreases as we move further away from the mean.

The factor \(\frac{1}{\sqrt{2\pi \sigma^2}}\) is the normalization constant. To ensure that the total probability across all values of \(x\) is equal to 1, we integrate the PDF across the entire real line:

This is a standard result, but the key point is that the normalization factor ensures that the area under the curve sums to one, thereby giving us a valid probability distribution.

Extending to Multivariate Gaussian Distribution

Now that we have the foundation in place, let’s shift gears and consider the generalization of the univariate Gaussian to higher dimensions. In the multivariate case, we are no longer dealing with a single random variable, but rather a vector of random variables, say \(\mathbf{x} = [x_1, x_2, \dots, x_k]^T\). This vector \(\mathbf{x}\) can represent a collection of correlated random variables, and we want to model the joint distribution of these variables.

The multivariate Gaussian distribution generalizes the concept of the univariate normal distribution to \(k\)-dimensional space. The PDF for a multivariate Gaussian distribution is expressed as:

Here, \(\mathbf{x}\) is a \(k\)-dimensional vector representing the random variables, \(\mu\) is a \(k\)-dimensional mean vector, and \(\Sigma\) is a \(k \times k\) covariance matrix that encodes the relationships (correlations and variances) between the variables in \(\mathbf{x}\). The term \((\mathbf{x} - \mu)^T \Sigma^{-1} (\mathbf{x} - \mu)\) is a quadratic form, measuring the “distance” of the vector \(\mathbf{x}\) from the mean vector \(\mu\). This distance is weighted by the inverse of the covariance matrix, \(\Sigma^{-1}\), which accounts for the fact that the random variables may not be independent, i.e., they can have correlations with each other. The factor \(\frac{1}{(2\pi)^{k/2} \mid \Sigma \mid^{1/2}}\) is the normalization constant, and it ensures that the total probability across the entire \(k\)-dimensional space integrates to one.

The mean vector \(\mu = [\mu_1, \mu_2, \dots, \mu_k]^T\) represents the central location of the distribution in the \(k\)-dimensional space. This vector shifts the distribution from the origin, telling us where the “center” of the distribution lies. If all variables \(x_1, x_2, \dots, x_k\) were independent and identically distributed (i.i.d.), then each \(\mu_i\) would be the mean of the respective variable.

The covariance matrix \(\Sigma\) is the heart of the multivariate Gaussian. The diagonal elements of \(\Sigma\) represent the variances of the individual variables (i.e., how spread out each variable is), and the off-diagonal elements represent the covariances between pairs of variables. For example, \(\sigma_{ij}\) represents the covariance between \(x_i\) and \(x_j\). If this value is nonzero, it means that \(x_i\) and \(x_j\) are correlated. A covariance of zero indicates that the variables are independent.

One important feature of the multivariate Gaussian is that the covariance matrix must be positive semi-definite. This ensures that the quadratic form \((\mathbf{x} - \mu)^T \Sigma^{-1} (\mathbf{x} - \mu)\) is always non-negative and that the distribution behaves well.

The above three paragraphs also serve as a review of Chapter 0 of this column and will not be repeated here.

Demo

We’ll start by plotting the univariate Gaussian distribution (a bell curve), then move to the bivariate Gaussian (a 2D contour plot), and finally extend to the trivariate Gaussian (3D surface plot). By doing so, we can observe how the distribution evolves with increasing dimensionality.

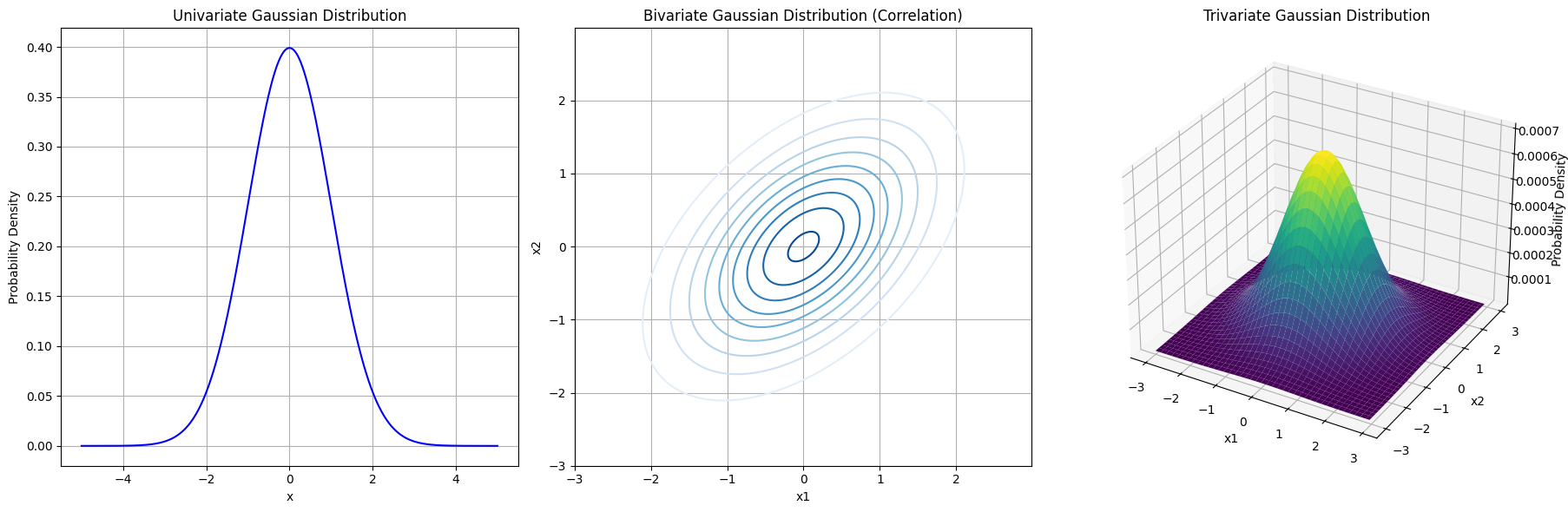
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
from mpl_toolkits.mplot3d import Axes3D

# --- Univariate Gaussian (1D) ---
mu = 0      # Mean
sigma = 1   # Standard deviation
x = np.linspace(-5, 5, 1000)  # Generate x values
pdf_1d = (1/np.sqrt(2*np.pi*sigma**2)) * np.exp(-0.5 * (x - mu)**2 / sigma**2)  # PDF

# --- Bivariate Gaussian (2D) ---
mu_2d = [0, 0]  # Mean vector
Sigma_2d = [[1, 0.5], [0.5, 1]]  # Covariance matrix with correlation
x2, y2 = np.mgrid[-3:3:.01, -3:3:.01]  # Create grid for 2D plot
pos_2d = np.dstack((x2, y2))  # Combine x2, y2 for the grid points
rv_2d = multivariate_normal(mu_2d, Sigma_2d)  # Multivariate normal distribution
pdf_2d = rv_2d.pdf(pos_2d)  # Compute the PDF

# --- Trivariate Gaussian (3D) ---
mu_3d = [0, 0, 0]  # Mean vector for 3D
Sigma_3d = np.diag([1, 1, 1])  # Covariance matrix (diagonal, no correlation)
x3, y3, z3 = np.mgrid[-3:3:.05, -3:3:.05, -3:3:.05]  # Create 3D grid
pos_3d = np.vstack([x3.ravel(), y3.ravel(), z3.ravel()]).T  # Flatten grid for 3D plotting
rv_3d = multivariate_normal(mu_3d, Sigma_3d)  # Multivariate normal distribution
pdf_3d = rv_3d.pdf(pos_3d).reshape(x3.shape)  # Compute the PDF for 3D

# --- Plotting ---
fig = plt.figure(figsize=(18, 6))

# 1D plot
ax1 = fig.add_subplot(131)
ax1.plot(x, pdf_1d, label=r'$\mathcal{N}(0, 1)$', color='blue')
ax1.set_title('Univariate Gaussian Distribution')
ax1.set_xlabel('x')
ax1.set_ylabel('Probability Density')
ax1.grid(True)

# 2D plot
ax2 = fig.add_subplot(132)
ax2.contour(x2, y2, pdf_2d, levels=10, cmap='Blues')
ax2.set_title('Bivariate Gaussian Distribution (Correlation)')
ax2.set_xlabel('x1')
ax2.set_ylabel('x2')
ax2.grid(True)

# 3D plot
ax3 = fig.add_subplot(133, projection='3d')
ax3.plot_surface(x3[:, :, 0], y3[:, :, 0], pdf_3d, cmap='viridis', edgecolor='none')
ax3.set_title('Trivariate Gaussian Distribution')
ax3.set_xlabel('x1')
ax3.set_ylabel('x2')
ax3.set_zlabel('Probability Density')

# Show all plots
plt.tight_layout()
plt.show()

Deriving the Normalization Constant

The most mathematically involved part of deriving the multivariate Gaussian distribution is ensuring that the PDF is normalized correctly. That is, we need to confirm that:

This normalization can be tricky due to the presence of the covariance matrix \(\Sigma\). The solution lies in diagonalizing the covariance matrix using an eigenvalue decomposition. The covariance matrix \(\Sigma\) can be written as:

where \(V\) is the matrix of eigenvectors and \(\Lambda\) is the diagonal matrix of eigenvalues. By changing variables to the eigenbasis of \(\Sigma\), we transform the quadratic form into a simpler form, and we can compute the necessary integrals.

In the new coordinates, the quadratic form becomes:

where \(\lambda_i\) are the eigenvalues of \(\Sigma\) and \(y_i\) are the transformed variables. Each integral of the form:

is a standard Gaussian integral, which evaluates to \(\sqrt{2\pi \lambda_i}\). The product of these integrals gives the normalization constant, and when combined with the volume scaling factor \(\mid\Sigma\mid^{1/2}\), we arrive at the final form of the PDF.

Thus, the normalization constant becomes:

This ensures that the total probability is indeed 1, completing the derivation of the multivariate Gaussian distribution.